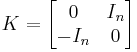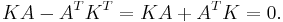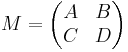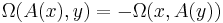Hamiltonian matrix

In mathematics, a Hamiltonian matrix $A$ is any real $2 n \times 2 n$ matrix $A$ that satisfies the condition that $KA$ is symmetric, where $K$ is the skew-symmetric matrix

$K= \begin{bmatrix} 0 & I_n \\ -I_n & 0 \\ \end{bmatrix}$

and $I n$ is the $n \times n$ identity matrix. In other words, $A$ is Hamiltonian if and only if

$KA - A^T K^T = KA %2B A^T K = 0.\,$

In the vector space of all $2 n \times 2 n$ matrices, Hamiltonian matrices form a subspace of dimension $2 n 2 + n$ .

1 Properties
2 Hamiltonian operators
3 See also
4 References
5 Notes

Properties

Let $M$ be a $2 n \times 2 n$ block matrix given by

$M = \begin{pmatrix}A & B \\ C & D\end{pmatrix}$

where

A

B

C

, and

D

are

n \times n

matrices. Then

M

is a Hamiltonian matrix provided that the matrices

B

and

C

are symmetric, and that

A + D T = 0

The transpose of a Hamiltonian matrix is Hamiltonian.
The trace of a Hamiltonian matrix is zero.
The commutator of two Hamiltonian matrices is Hamiltonian.
The eigenvalues of any Hamiltonian matrix are symmetric about the imaginary axis.
The space of all Hamiltonian matrices is a Lie algebra 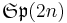${\mathfrak{Sp}}(2n)$ .^[1]

Hamiltonian operators

Let $V$ be a vector space, equipped with a symplectic form $Ω$ . A linear map 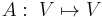$A:\; V \mapsto V$ is called a Hamiltonian operator with respect to $Ω$ if the form 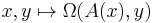$x, y \mapsto \Omega(A(x), y)$ is symmetric. Equivalently, it should satisfy

$\Omega(A(x), y)=-\Omega(x, A(y))$

Choose a basis $e 1, ... e 2 n$ in $V$ , such that $Ω$ is written as 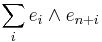$\sum_i e_i \wedge e_{n%2Bi}$ . A linear operator is Hamiltonian with respect to $Ω$ if and only if its matrix in this basis is Hamiltonian.^[2]

From this definition, the following properties are apparent. A square of a Hamiltonian matrix is skew-Hamiltonian. An exponential of a Hamiltonian matrix is symplectic, and a logarithm of a symplectic matrix is Hamiltonian.

References

Meyer, K. R.; Hall, G. R. (1991). Introduction to Hamiltonian dynamical systems and the N-body problem. Springer. pp. 34–35. ISBN 0-387-97637-X.

Notes

^ Dragt, Alex J. (2005), "The symplectic group and classical mechanics", Annals of the New York Academy of Sciences 1045 (1): 291–307, doi:10.1196/annals.1350.025 .
^ Waterhouse, William C. (2005), "The structure of alternating-Hamiltonian matrices", Linear Algebra and its Application 396: 385–390, doi:10.1016/j.laa.2004.10.003 .

Hamiltonian matrix

Contents

Properties

Hamiltonian operators

See also

References

Notes